Clasificación de los triángulos.

Los triángulos se clasifican según distintas características geométricas dando lugar a tres tipos de clasificación:

• según su configuración
• según las medidas de los lados
• según las medidas de los ángulos.

Vamos a ver más de cerca cada uno de estos tipos de clasificación.
Podemos clasificar los triángulos según su configuración en:

• Rectilíneos
• Curvilíneos
• Mixtilíneos

Podemos clasificar los triángulos según las medidas de los lados en:

• Equilátero
• Isósceles
• Escaleno

Observamos los distintos tipos a los que da lugar esta clasificación en el siguiente dibujo


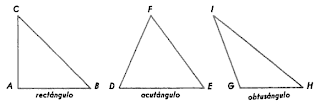
Por último podemos clasificar los triángulos según las medidas de los ángulos en:

• Rectángulo
• Acutángulo
• Obtusángulo

Observamos los distintos tipos a los que da lugar esta clasificación en el siguiente dibujo

Triángulos: Definición y Clasificación

El triángulo es una figura o superficie plana limitado por tres rectas que se cortan dos a dos. Tiene tres lados y tres ángulos.

Los puntos de intersección de las rectas se llaman vértices y los segmentos comprendidos entre los vértices se llaman lados.

Los vértices se designan con letras mayúsculas y los lados con letras minúsculas, utilizando la misma letra del vértice opuesto.

Vamos a considerar algunas de sus propiedades geométricas fundamentales:

• La suma de los tres ángulos interiores es 180º.
• La suma de los ángulos exteriores es 360º.
• Un lado es siempre menor que la suma de los otros dos lados.
• En todo triángulo la suma de las dos bisectrices exterior e interior forma 90º.
• En un triángulo rectángulo la hipotenusa es mayor que cada uno de sus catetos.

El triángulo como polígono

Debemos comenzar el estudio geométrico del triángulo considerándolo como el más sencillo de los polígonos.
Así, vamos a considerar algunas de las características básicas de los polígonos que nos ayudarán posteriormente a comprender mejor las características del triángulo.
Un polígono viene definido como la porción del plano limitada por rectas que se cortan o bien como el espacio limitado por una línea quebrada, cerrada y plana.
Cada segmento de la línea quebrada se llama lado y los puntos de intersección de los lados se llaman vértices.

• Un polígono es cóncavo si al trazar cualquier recta sólo lo corta en dos puntos.
• El polígono es convexo si existe alguna recta que lo corte en más de dos puntos.

Se dice que un polígono está inscrito en una circunferencia si todos sus vértices están en ella.



El polígono está circunscrito si todos sus lados son tangentes a la circunferencia.